Iteration: Loops vs Functional Programming

Iterative processes are characterized by successive steps forming a sequence of states captured by state variables. In each step the state variables are updated based on themselves and some rule. Iteration is often implemented using control-flow constructs like the for or while loop (see ?Control for help).

The functional programming paradigm offers an alternative vocabulary for iteration—as well as for other types of processes—based on some possibly generic vector. That vector, often a list, provides a conventional interface for certain higher order functions (see ?base::Reduce for help). These higher order functions all enumerate the components of the vector and apply to each component some other function which they receive as argument. Depending on the return value of that function argument and the number of its arguments, such a higher order function may play a number of roles:

filter, e.g. Filter, where the function argument has logical value (predicate)
map, e.g. Map and lapply, where the function argument acts as a unary operator on single components of the vector
accumulator, e.g. Reduce, where the function argument acts as a binary operator on pairs of objects derived from the vector

A general syntax and semantics is illustrated below (figure source here). Note that the R-specific syntax uses uppercase initials: Filter, Map, Reduce.

Fig

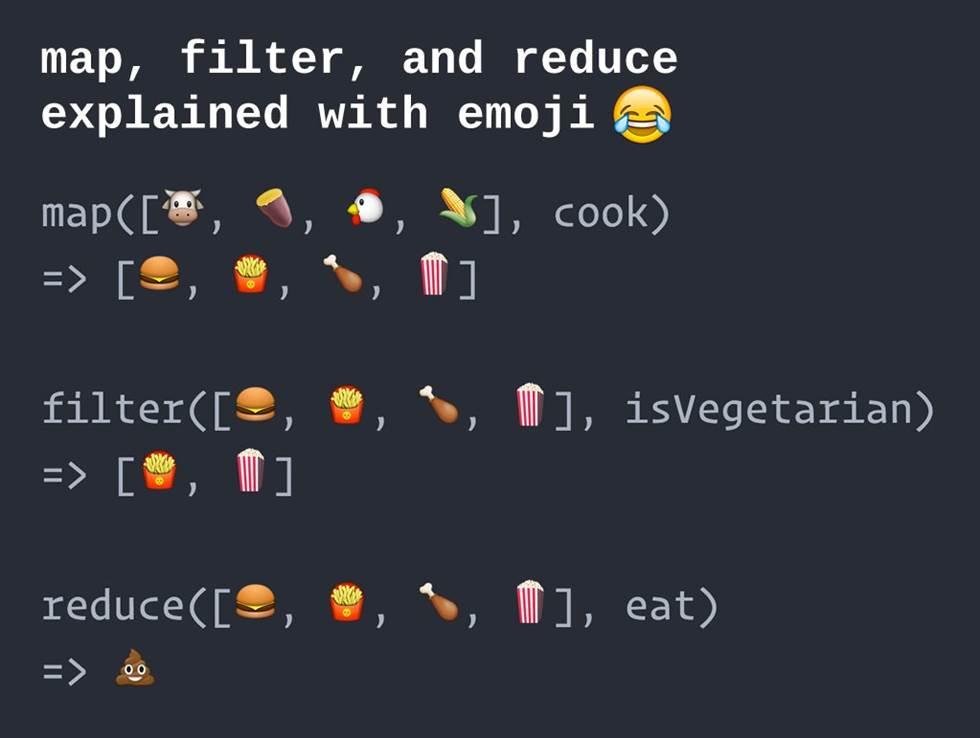
In what follows a toy problem will be solved iteratively either with a for loop or with the accumulator Reduce to highlight shared features and differences between the two strategies. The toy problem will also illustrate that Reduce can deal with generalized vectors—in the case a list of data frames.

The problem

Suppose we want to turn the input vector $v$ into the output vector $w$ such that

# this is not R code
v = (T,F,F,T,T,F,F,F,F,F,F,F,T,F,F,F,T,T,T,T,T,F,F,F,F,T,F,F,T,T) # input
w = (1,0,0,2,2,0,0,0,0,0,0,0,3,0,0,0,4,4,4,4,4,0,0,0,0,5,0,0,6,6) # desired output

To generalize the problem, let the input vector $v$ be a (finite) sequence taking values on the binary set, say $\{\mathrm{true},\mathrm{false}\}$ whereas the output vector $w$ a sequence on integers with the following properties:

$w$ is of the same length as $v$
$w_i=0$ if $v_i=\mathrm{false}$ ; otherwise $w_i>0$
for the $m$ -th contiguous subsequence of $v$ such that $v_i=v_{i+1}=...=v_{i+k}=\mathrm{true}$ and $v_{i-1}=v_{i+k+1}=\mathrm{false}$ , where $k\ge 1$ , the corresponding subsequence of $w$ is $w_i=w_{i+1}=...=w_{i+k}=m$

We will refer to such “all-true” subsequences of $v$ as $T$ -segments and the “all-false” subsequences between them as $F$ -segments.

Motivating examples

This problem often arises in conjunction with longitudinal data, where we observe a sequence $v_1,...,v_n$ , where each $v_i$ is a binary class label. For example, $i$ might indicate a nucleotide site within the coding region of a gene and $v_i$ whether that site is within an exon or an intron. Then the goal would be to uniquely label the exons (but not the introns). Another genetic example is when each $i$ is a gene and $v_i$ indicates whether $i$ is part of some imprinted gene cluster. Then the goal would amount to uniquely label the clusters.

Data preparation

# made up data
v <- c(T, F, F, T, T, F, F, F, F, F, F, F, T, F, F, F, T, T, T, T, T, F, F, F, F, T, F, F, T, T)

Solution with a loop

Consider the function

T.seg.loop <- function(v) {
    w <- w.j <- as.integer(v[1]) # initialize
    for(i in seq(2, length(v))) {
        if(! v[i]) w <- c(w, 0)  # i is in an F-segment
        else {                   # i is in a T-segment
            if(! v[i - 1])       # i is at the start of a T-segment
                w.j <- w.j + 1
            w <- c(w, w.j)
        }
    }
    return(data.frame(v = v, w = w))
}

The iterative strategy expressed by T.seg.loop is to visit each $v_i$ sequentially $i=1,...,n$ and compute $w_i$ given $v_i$ and the preceding $v_{i-1}$ . But besides $v_{i-1},v_i$ another piece of information is necessary: the number of $T$ -segments occurring up to $i-1$ i.e in the subsequence $v_1,...,v_{i-1}$ , which is the same as the value of $w_j$ , where $j$ indicates the start of the last $T$ -segment in $v_1,...,v_{i-1}$ referred to henceforth as the latest $T$ -segment.

Note that $j\lt i$ and $v_{i-1}$ may or may not be part of the latest $T$ -segment. In both cases $w_i=0$ if $v_i=\mathrm{false}$ otherwise $w_i$ differs between the two cases: If $v_{i-1}$ is in the latest $T$ -segment then so is $v_i$ and thus $w_i=w_j$ ; but if $v_{i-1}$ is in the latest $F$ -segment then $v_i$ begins a new $T$ -segment, therefore $w_i=w_j+1$ .

As we see, the strategy works:

T.seg.loop(v)

##        v w
## 1   TRUE 1
## 2  FALSE 0
## 3  FALSE 0
## 4   TRUE 2
## 5   TRUE 2
## 6  FALSE 0
## 7  FALSE 0
## 8  FALSE 0
## 9  FALSE 0
## 10 FALSE 0
## 11 FALSE 0
## 12 FALSE 0
## 13  TRUE 3
## 14 FALSE 0
## 15 FALSE 0
## 16 FALSE 0
## 17  TRUE 4
## 18  TRUE 4
## 19  TRUE 4
## 20  TRUE 4
## 21  TRUE 4
## 22 FALSE 0
## 23 FALSE 0
## 24 FALSE 0
## 25 FALSE 0
## 26  TRUE 5
## 27 FALSE 0
## 28 FALSE 0
## 29  TRUE 6
## 30  TRUE 6

But from the present viewpoint what is important is how T.seg.loop implements iteration

for enumerates a components of an integer vector generated by sec
i, v[i] and w.j and w play the role of state variables
the expressions w <- c(w, 0) and w <- c(w, w.j) together with the for loop accumulate the result
updating v[i] and hence w.j and w require the entire v to be available within T.seg.loop
enumeration, updating and accumulation are all tied to a single control-flow construct
the two expressions of accumulation are scattered in different parts of the for loop

As a result of last two characteristics T.seg.loop is concise but “monolithic” hence conceptually convoluted, which would hinder its analysis and debugging (if it were necessary). To achieve a more modular design, we turn to functional programming.

Solution using the functional paradigm

Instead of immediately presenting T.seg.funprog, the functional counterpart of T.seg.loop, in its complete form, I build it piece-by-piece, demonstrating modularity. I begin by reformulating the problem for a reason to become clear shortly. While the ultimately aim is $w=(1,0,0,2,0,0,...)$ it will be useful to first compute a vector $z=(1,-1,-1,2,-2,-2,...)$ . Under our toy example

# this is not R code
v = (T, F, F,T,T, F, F, F, F, F, F, F,T, F, F, F,T,T,T,T,T, F, F, F, F,T,F, F,T,T) # input
z = (1,-1,-1,2,2,-2,-2,-2,-2,-2,-2,-2,3,-3,-3,-3,4,4,4,4,4,-4,-4,-4,-4,5,5,-5,6,6) # desired output

Once $z$ is computed then it is easy to obtain the desired $w$ using the function

do.zero <- function(z)
    ifelse(z > 0, z, 0)

$z$ crucially differs from $w$ in that not only each $T$ -segment but also each $F$ -segment has its unique label, a non-positive integer. (Note that the label of the first $F$ -segment would be zero both for $w$ and $z$ if $v$ didn’t begin with a $T$ .) Therefore, in the $i$ -th step of an iterative process $z_i$ can be updated solely from $z_{i-1}$ and $v_i$ . In contrast updating of $w_i$ requires not only $w_{i-1}$ and $v_i$ but also an additional state variable; in the case of T.seq.loop this was the role of w.j.

Now we need the following:

a procedure that updates $z_i$ given $z_{i-1}$ and $v_i$
an accumulator using that procedure

Before addressing the first point, it will be convenient to initialize the data frame that will hold $v$ and the desired $z$

df <- data.frame(v = v)
df$z <- integer(length(df$v))
df$z[1] <- as.integer(df$v[1])

It will also be convenient to restructure the data frame df into the list l.df, whose components are single-row data frames each representing row of df.

l.df <- lapply(seq_len(nrow(df)), function(i) df[i, ])
l.df[1:2]

## [[1]]
##      v z
## 1 TRUE 1
## 
## [[2]]
##       v z
## 2 FALSE 0

The procedure updating $z_i$ is

T.seg.binop <- function(A, B) {
    last.A <- A[nrow(A), ] # last row of A
    helper <- function() { # returns z for B
        if(last.A$v) {
            if(B$v) last.A$z
            else - last.A$z
        } else {
            if(B$v) 1 - last.A$z
            else last.A$z
        }
    }
    B$z <- helper() # replace initial z with correct z
    rbind(A, B) # append B to the end of A
}

The name expresses that T.seq.binop is a binary operator taking two data frames A and B returns a single data frame third one by modifying B and appending that to A. Less important is that $z_i$ is actually computed slightly more conveniently from $z_{i-1}$ and $v_i$ and $v_{i-1}$ than from only $z_{i-1}$ and $v_i$ because the latter would require checking if $z_{i-1}\lt 0$ .

A suitable accumulator is already implemented in base::Reduce. Now we are ready to compute $z$

df <- Reduce(T.seg.binop, l.df)
df$z

##  [1]  1 -1 -1  2  2 -2 -2 -2 -2 -2 -2 -2  3 -3 -3 -3  4  4  4  4  4 -4 -4
## [24] -4 -4  5 -5 -5  6  6

Putting everything together

T.seg.funprog <- function(v, F.as.zero = TRUE, ...) {
    df <- data.frame(v = v)
    df$z <- integer(length(df$v))
    df$z[1] <- as.integer(df$v[1])
    df <- Reduce(T.seg.binop, lapply(seq_len(nrow(df)), function(i) df[i, ]), ...)
    if(F.as.zero)
        data.frame(v = v, w = do.zero(df$z))
    else df
}

This function gives the same answer as its loop-based counterpart.

all.equal(T.seg.funprog(v), T.seg.loop(v))

## [1] TRUE

Yet, T.seg.funprog is rather different from T.seg.loop in that

enumeration and accumulation is implemented in Reduce and is done directly on l.df instead of an auxiliary integer vector
no separate state variables (like w.j in T.seg.loop) are needed because the state of the process at each step is represented by the state of the accumulating result
a separate binary operator T.seg.binop updates the state independently of the enumerator/accumulator T.seg.loop

Conclusion

In case of this toy problem the functional programming approach appears conceptually more pleasing due to its modularity. On the other hand, it required longer code, multiple functions, the division of a single problem (finding $w$ given $v$ ) into two sub problems (finding $z$ given $v$ and $w$ given $z$ ), and restructuring the initial data frame df into the list l.df.

Epilogue: What is accumulation?

The accumulator Reduce in T.seq.funprog takes the generalized vector l.df and accumulates the value of T.seg.binop called in successive steps. In the $i$ -th step the A argument to T.seg.binop is the value of the same function at the $i-1$ -th step and the B argument is the $i$ -th component of l.df, that is l.df[[i]]. In the final step T.seg.binop(A, B) evaluates to the desired data frame.

By default Reduce returns only that final result. However, Reduce can can additionally return the successive intermediate results when called with the accumulate = TRUE argument. The terminology might sound confusing but with the default accumulate = FALSE argument Reduce is still considered an accumulator. Setting terminology aside, calling Reduce in T.seg.funprog with accumulate = TRUE evaluates to a list of data frames, each component showing the state of the iterative process at the corresponding step:

T.seg.funprog(v, F.as.zero = FALSE, accumulate = TRUE)[1:3]

## [[1]]
##      v z
## 1 TRUE 1
## 
## [[2]]
##       v  z
## 1  TRUE  1
## 2 FALSE -1
## 
## [[3]]
##       v  z
## 1  TRUE  1
## 2 FALSE -1
## 3 FALSE -1

Given the above definition of T.seg.binop the only use of accumulate = TRUE in solving this toy problem is only didactic. But suppose we had a version of T.seg.binop, say T.seg.binop.2, that returns only the modified B without appending it to A. In that case accumulate = TRUE would be necessary to obtain the desired result. But then Reduce would evaluate to a list of one-row data frames—the updated version of l.df. So that value would have to be restructured to obtain single data frame by another round of accumulation, this time with the binary operator expressed by the rbind function. Therefore T.seg.funprog would have to be modified as

T.seg.funprog <- function(v, F.as.zero = TRUE, ...) {
    df <- data.frame(v = v)
    df$z <- integer(length(df$v))
    df$z[1] <- as.integer(df$v[1])
    # beginning of modification
    l.df <- Reduce(T.seg.binop.2, lapply(seq_len(nrow(df)), function(i) df[i, ]), ...)
    df <- Reduce(rbind, l.df)
    # end of modification
    if(F.as.zero)
        data.frame(v = v, w = do.zero(df$z))
    else df
}